RAID technology helps businesses manage their hard drive storage in a variety of ways. By deploying multiple drives in a RAID configuration in a single array, storage teams can employ protective, performative or restorative technologies for hard disk drives (HDDs).
If your business is considering implementing a RAID array, learn more about each of the major configurations to decide which would be best for your organization. This guide highlights the design of each of the most popular RAID configurations as well as their advantages and disadvantages.
RAID levels explained
- What is RAID storage?
- How does RAID work?
- What are the implementation types of RAID?
- What are the different RAID levels?
- Bottom line: Effectively using RAID in your business
What is RAID storage?
RAID stands for Redundant Array of Independent Disks. It’s a storage technology designed to improve the fault tolerance of hard drives. RAID is implemented in arrays of at least two disks that work together. The exact number of disks is dependent upon the specific implementation.
Different RAID configurations provide different benefits to enterprise storage systems. While RAID can be a helpful fault tolerance tool, it is not suitable to replace backup solutions. Some RAID implementations can withstand only one disk failure and don’t allow much room for natural or unexpected hardware problems.
How does RAID work?
This depends on the specific implementation of RAID, but generally speaking, two or more disks work together to improve data read-and-write performance. A RAID controller or a driver is used to manage the disks. RAID use three main approaches—striping, mirroring, and parity—depending upon the configuration. Some RAID configurations improve performance, while others increase fault tolerance. Some do both. We’ll look at all three approaches in more detail later in this article.
What are the implementation types of RAID?
RAID storage has three standard implementation methods: hardware, software, and firmware.
Hardware RAID
A dedicated hardware controller provides hardware-based RAID services. IT can deploy hardware RAID two ways—an external RAID Controller Card or an internal RAID-on-Chip:
- A RAID Controller Card is a plug-in expansion card that connects to a PCIe or PCI-X motherboard slot. The card contains a RAID processor and Input/Output processors, a specialized processor that loads and stores data into memory and executes instructions, with drive interfaces. The cards are expensive, but since they are independent of the host, all RAID operations are offloaded from the CPU to the dedicated card.
- RAID-on-Chip is a single chip on the motherboard that integrates the host interface, I/O interfaces for HDDs, the RAID processor and a memory controller.
Software RAID
Software-based RAID delivers RAID services from the host. Software RAID comes in two flavors: pure software-defined, which runs from the Operating System (OS), and hybrid software that contains a hardware component to relieve the load on the CPU:
- Software-Only RAID is the least expensive of the RAID types. Often included as a native function on the OS, it’s a host-based software application that manages RAID calculations for attached hard disk drives. It’s attached via a Host Bus Adapter (HBA) or native I/O interface and activates when the OS loads the RAID driver.
- Hybrid RAID, which is still software-based, uses a hardware component to deliver RAID BIOS functions from RAID BIOs on the motherboard or on an HBA. This technology offers a layer of redundant protection from a faulty boot process. Software-only RAID boots from the operating system, and boot errors could affect the entire RAID subsystem. The addition of a RAID BIOS hardware component protects the subsystem from operating system boot errors.
Firmware-Based RAID
Firmware-based RAID is pre-configured within the relevant computer. Typically, the RAID chip is installed on the computer’s motherboard. Unlike software RAID, it’s only implemented when the computer’s OS first boots. Like software-based RAID, because the RAID controls are connected to the computer’s operating system, it may be slower than hardware-based RAID if the OS is performing other resource-intensive tasks or is infected by malware.
Different RAID levels explained
Whether hardware or software, RAID is available in different schemes, or RAID levels. The most commonly used levels are RAID 0, 1, 5, 6, and 10. RAID 0, 1, and 5 work on both HDD and SSD media. RAID levels 4 and 6 also work on both media but are rarely seen in practice: RAID 4 has slow write speeds because of parity, as does RAID 6 when performing intensive write operations. Additionally, RAID levels 2 and 3 are outdated and rarely implemented.
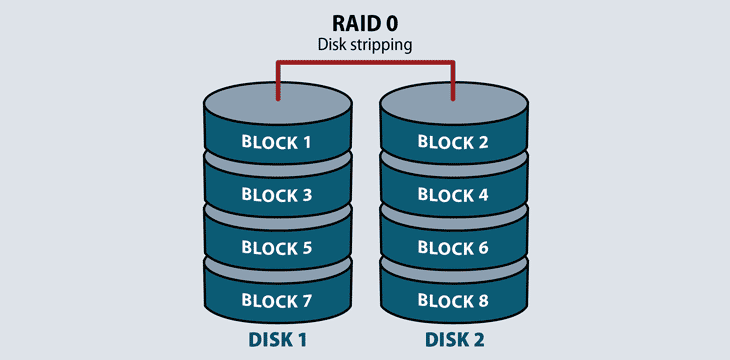
RAID 0
Requiring a minimum of two disks, RAID 0 splits files and stripes the data across two disks or more, treating the striped disks as a single partition. Because striping technology distributes data across multiple disks in an array, reading one file requires reading multiple disks.
RAID 0 does not provide redundancy or fault tolerance. Since it treats multiple disks as a single partition, if even one drive fails, the striped file is unreadable. This is not an insurmountable problem in video streaming or computer gaming environments where performance matters the most, and the source file will still exist even if the stream fails. However, it is a problem in high-availability environments.
Advantages
RAID 0 is beneficial because of its speed. Because multiple hard drives are reading and writing parts of the same file at the same time, throughput is generally faster.
Disadvantages
RAID 0’s lack of fault tolerance makes it unreliable for supporting important applications and untenable for backing up any environments.
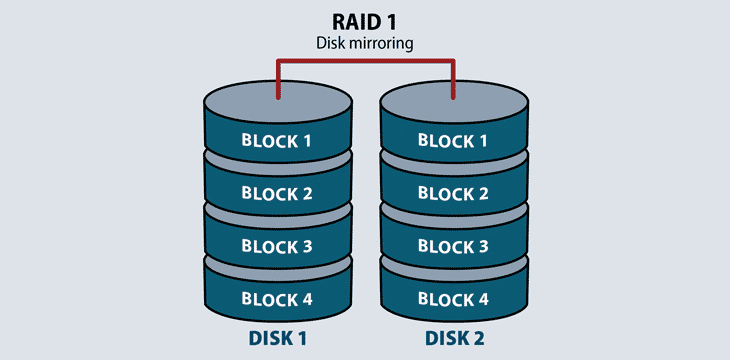
RAID 1
RAID 1 uses disk mirroring to provide data redundancy and failover. It reads and writes the exact same data to each disk. Should a mirrored disk fail, the file exists in its entirety on the functioning disk. Once IT replaces the failed disk, the RAID system will automatically mirror back to the replacement drive. RAID 1 also increases read performance.
RAID 1 requires a minimum of two disks to work. It does take up more usable capacity on drives, but is an economical failover process on application servers.
Advantages
By copying one disk to another, RAID 1 decreases the chance of total data loss from a disk failure.
Disadvantages
Because two disks store the same data, RAID 1 can only use half of the array’s total storage.
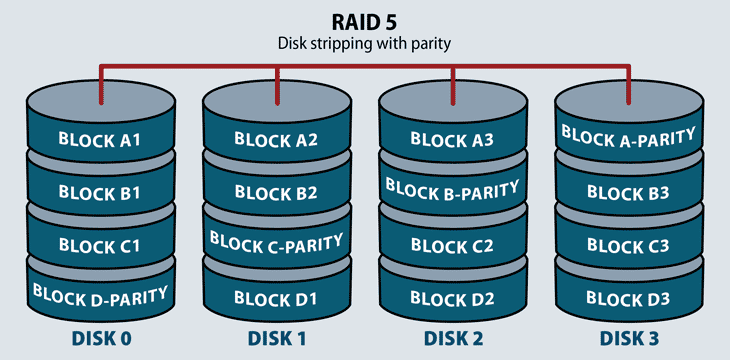
Raid 5
RAID 5 distributes striping and parity at a block level. Parity is raw binary data–the RAID system calculates its values to create a parity block, which the system uses to recover striped data from a failed drive. Most RAID systems with parity functions store parity blocks on the disks in the array. Some RAID systems also dedicate a disk to parity calculations, but these are rare.
RAID 5 stores parity blocks on striped disks. Each stripe has its own dedicated parity block. RAID 5 can withstand the loss of one disk in the array.
RAID 5 combines the performance of RAID 0 with the redundancy of RAID 1, but takes up a lot of storage space to do it—about one third of usable capacity. This level increases write performance since all drives in the array simultaneously serve write requests. However, overall disk performance can suffer from write amplification, since even minor changes to the stripes require multiple steps and recalculations.
Advantages
- RAID 5’s striping increases read performance.
- Parity improves data accuracy.
- RAID 5 can be used for SSDs as well as hard drives. But be careful to pick SSDs that are the exact same age in case they fail at the same time.
Disadvantages
RAID 5 only has fault tolerance for one disk failure.
Read more about RAID 5 and its benefits for both HDDs and SSDs.
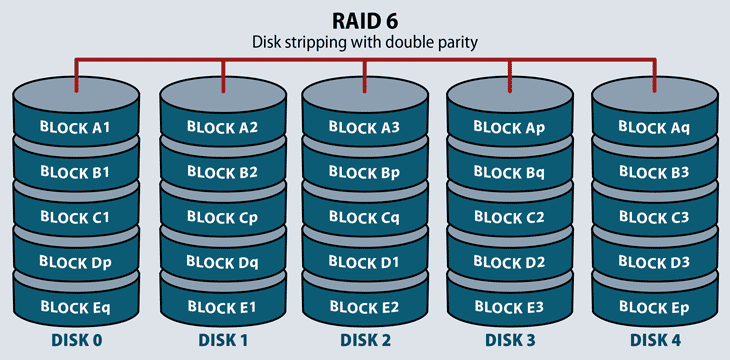
RAID 6
This RAID level operates like RAID 5 with distributed parity and striping. The main operational difference in RAID 6 is that there is a minimum of four disks in a RAID 6 array, and the system stores an additional parity block on each desk. This enables a configuration where two disks may fail before the array is unavailable. Its primary uses are application servers and large storage arrays.
RAID 6 offers higher redundancy and increased read performance over RAID 5. It can suffer from the same server performance overhead with intensive write operations. This performance hit depends on the RAID system architecture: hardware or software, if it’s located in firmware, and if the system includes processing software for high-performance parity calculations.
Advantages
- RAID 6 arrays can withstand two drive failures because they have two instances of parity rather than a single one.
- RAID 6 has better read performance than RAID 5.
Disadvantages
- RAID 6 is more expensive than some other forms of RAID.
- Rebuilding data on larger RAID 6 arrays can be a slow process.
Learn more about the differences between RAID levels 5 and 6.
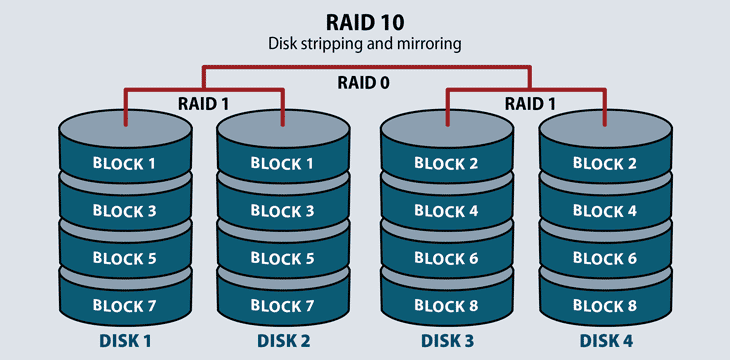
RAID 10: Striping and Mirroring
RAID 10 requires a minimum of four disks in the array. It stripes across disks for higher performance, and mirrors for redundancy. In a four-drive array, the system stripes data to two of the disks. The remaining two disks mirror the striped disks, each one storing half of the data. RAID 10 combines the benefits of RAID 0 and RAID 1: faster read times and some redundancy through mirroring.
This RAID level serves environments that require both high data security and high performance, such as high transactional databases that store sensitive information. It’s the most expensive of the RAID levels, with lower usable capacity and high system costs.
Advantages
- RAID 10 rebuilds data more quickly than other RAID implementations.
- RAID 10 has fast overall read operations.
Disadvantages
- RAID 10 is the most expensive variation of RAID.
- Fault tolerance is only one disk, unlike RAID 6.
Bottom line: Effectively using RAID in your business
Before implementing RAID, consider your storage team’s top priorities. Are you more focused on cost-effectiveness, or do you need high performance? This will likely depend on the applications that RAID is supporting.
Keep in mind that fault tolerance shouldn’t be thrown to the side just to have fast hard drive performance. Perhaps the most important part of using RAID is not relying on it for data protection. RAID is an initial layer of fault tolerance, but it can withstand at most two drive failures. To protect the data on your hard disks, implement additional backup strategies.
Read more about the best backup solutions for businesses.